Inference on Tables as Semi-structured Data

About

Understanding ubiquitous semi-structured tabulated data requires not only comprehending the meaning of text fragments, but also implicit relationships between them. We argue that such data can prove as a testing ground for understanding how we reason about information. To study this, we introduce a new dataset called INFOTABS, comprising of human-written textual hypotheses based on premises that are tables extracted from Wikipedia info-boxes. Our analysis shows that the semi-structured, multi-domain and heterogeneous nature of the premises admits complex, multi-faceted reasoning.

tldr: INFOTABS is a Semi-structured inference dataset with wikipedia Infobox tables as premise and human written statements as hypothesis.

Procedure

We use Amazon Mechanical Turk (mturk) for data collection and validation. Annotators were presented with a tabular premise (infobox tables) and instructed to write three self-contained grammatical sentences based on the tables: one of which is true given the table, one which is false, and one which may or may not be true. We provide detailed instructions with illustrative examples using a table and also general principles to bear in mind (refer to template). For each premise-hypothesis in the development and the test sets, we also asked five turkers to predict whether the hypothesis is entailed or contradicted by, or is unrelated to the premise table for development and the three test splits (refer to template).

Example

Below is an inference example from the INFOTABS dataset. On the right is a premise which is a table extracted from wikipedia infobox. On the left are hypotheses written by human annotators. Here, colors

'green'

,

'gray'

, and

'red'

represent true (i.e., entailment), maybe true (i.e., neutral) and false (i.e., contradiction) statements, respectively.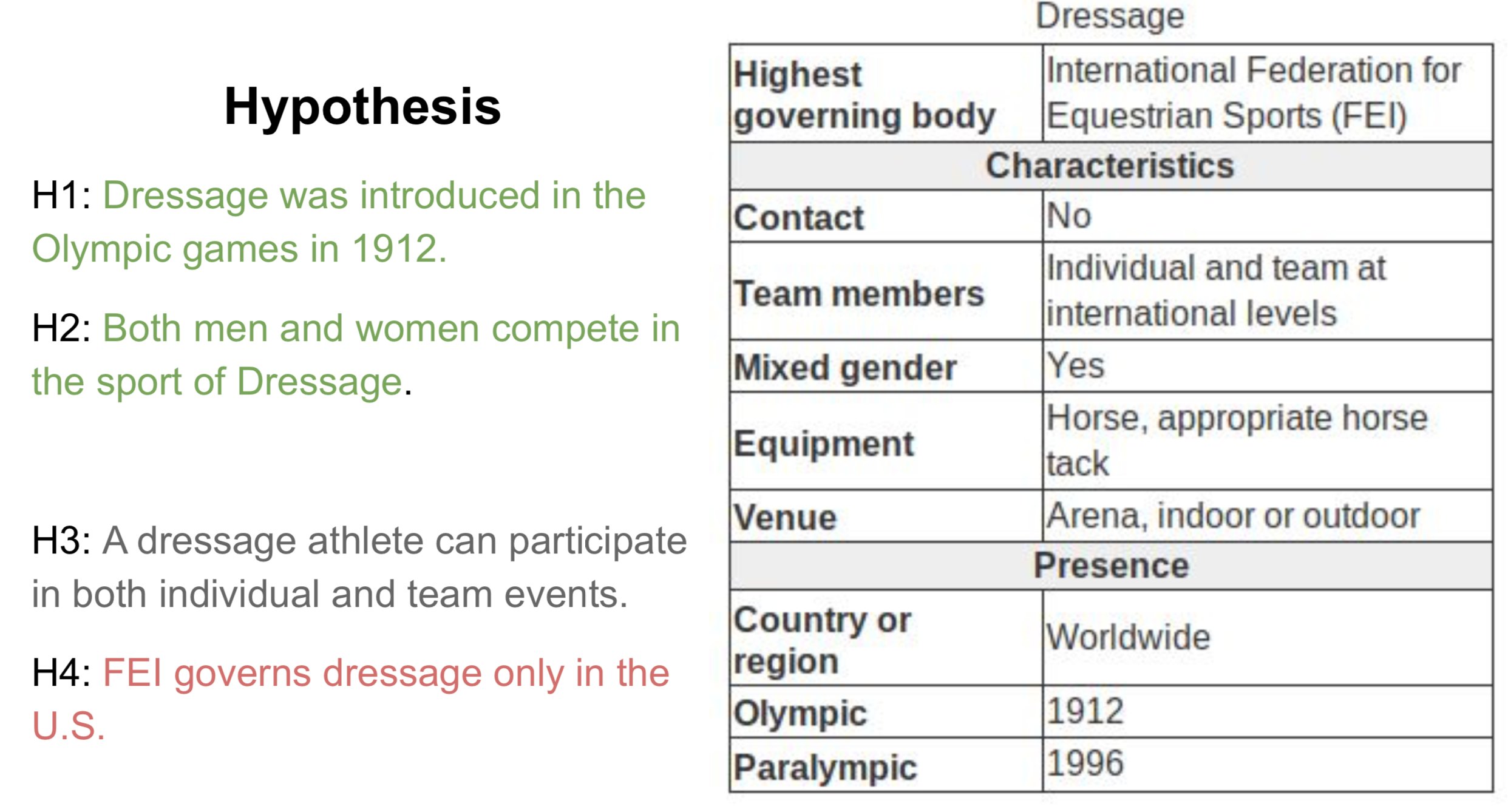

Reasoning

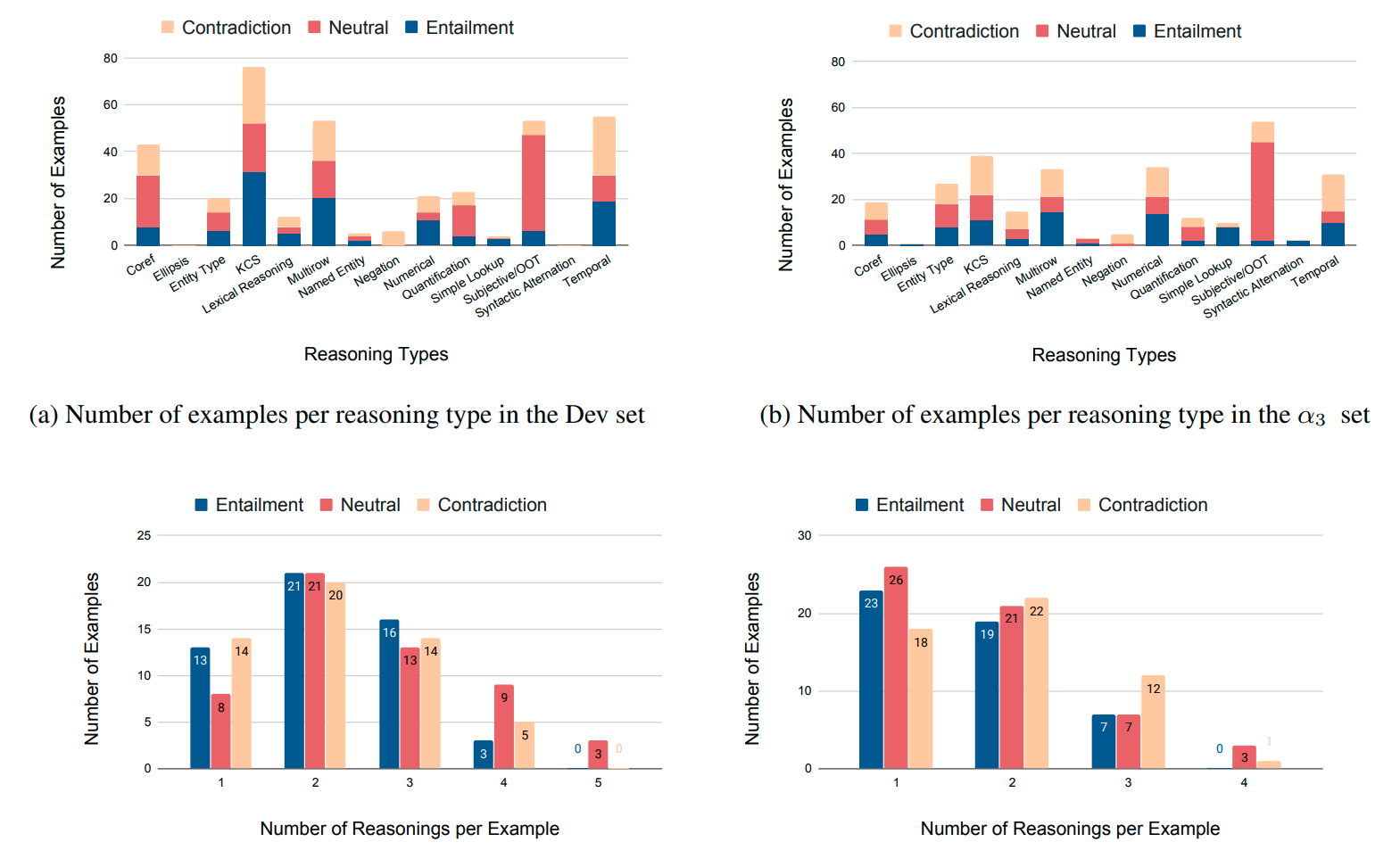
To study the nature of reasoning that is involved in deciding the relationship between a table and a hypothesis, we adapted the set of reasoning categories from GLUE Benchmark to table premises. All definitions and their boundaries were verified with several rounds of discussions. Following this, three graduate students (authors of the paper) independently annotated 160 pairs from the dev and alpha 3 test sets each, and edge cases were adjudicated to arrive at consensus labels.

Type and counts of reasoning in the Development and test alpha3 data splits. OOT and KCS are short forms of out-of-table and Knowledge & Common Sense, respectively.

Dataset Statistics

Our dataset consists of five splits (train, dev, alpha one, alpha two and alpha three). Below we provide basic statistics of data, i.e., number of tables and table-sentence pairs in each of the data splits. We also performed a validation step with five annotators for inter annotator agreement for all splits except the training set.

Data Split Number of Tables Number of Pairs
Train 1740 16538
Dev 200 1800
alpha 1 200 1800
alpha 2 200 1800
alpha 3 200 1800
Number of tables and premise-hypothesis pairs for each data split


Data Split Cohen's Kappa Human Performance Majority Agreeement
Dev 0.78 79.78 93.53
alpha 1 0.80 84.04 97.48
alpha 2 0.80 83.88 96.77
alpha 3 0.74 79.33 95.58
Cohen's Kappa, human baseline and inter-annotator agreement scores

Knowledge + InfoTabS

You should check our NAACL 2021 paper which enhance InfoTabS with extra Knowledge.

TabPert

You should check our EMNLP 2021 paper which is a tabular perturbation platform to generate counterfactual examples.

People

The INFOTABS dataset is prepared at the School of Computing of University of Utah by the following people:

From left to right, Vivek Gupta, Maitrey Mehta, Pegah Nokhiz and Vivek Srikumar.

Citation

Please cite our paper as below if you use the INFOTABS dataset.

@inproceedings{gupta-etal-2020-infotabs,
    title = "{INFOTABS}: Inference on Tables as Semi-structured Data",
    author = "Gupta, Vivek  and
      Mehta, Maitrey  and
      Nokhiz, Pegah  and
      Srikumar, Vivek",
    booktitle = "Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics",
    month = jul,
    year = "2020",
    address = "Online",
    publisher = "Association for Computational Linguistics",
    url = "https://www.aclweb.org/anthology/2020.acl-main.210",
    pages = "2309--2324",
    abstract = "In this paper, we observe that semi-structured tabulated text is ubiquitous; understanding them requires not only comprehending the meaning of text fragments, but also implicit relationships between them. We argue that such data can prove as a testing ground for understanding how we reason about information. To study this, we introduce a new dataset called INFOTABS, comprising of human-written textual hypotheses based on premises that are tables extracted from Wikipedia info-boxes. Our analysis shows that the semi-structured, multi-domain and heterogeneous nature of the premises admits complex, multi-faceted reasoning. Experiments reveal that, while human annotators agree on the relationships between a table-hypothesis pair, several standard modeling strategies are unsuccessful at the task, suggesting that reasoning about tables can pose a difficult modeling challenge.",
}

Acknowledgement

Authors thank members of the Utah NLP group for their valuable insights and suggestions at various stages of the project; and ACL 2020 reviewers for pointers to related works, corrections, and helpful comments. Authors thank the largest free resource Wikipedia for InfoTabS tables. We are also indebted to the many anonymous Turkers who helped craft the dataset. We acknowledge the support of the support of NSF Grants No. 1822877 and 1801446, and a generous gift from Google.